在原始的Rosenblatt感知器中,使用阶跃函数作为激活函数,只产生两个离散值。http://www.yifeiluo.cn/blog/3655/1-rosenblatt%e6%84%9f%e7%9f%a5%e5%99%a8/
分类: Notes(技术笔记)
0.神经网络发展概述
附件包括从Rosenblatt感知器到卷积神经网络、循环神经网络的代码实现,运行环境为python3.8.6,依赖库包括:numpy1.20.2、matplotlib3.4.1、keras2.4.3、tensorflow2.5.0,LSTM的预训练词向量体积过大需自行下载。
本篇算是机器学习相关技术总结的序章,但写在Rosenblatt感知器之后,是第二篇,重新梳理了叙述的逻辑。主要完成了对神经网络发展历史的梳理,以反向传播算法为分界,对BP算法之前的技术演进作较简要阐述,对之后的理论、算法、结构作简要概述,希望作为详细论述Rosenblatt感知器、卷积神经网络、循环神经网络等关键代表性模型之前的摘要,也作为激活函数、损失函数、优化算法等专题内容的背景铺垫。
1943年,Warren McCulloch和数学家Walter Pitts提出了神经元的首个简化数学模型,也就是McCulloch Pitts神经元模型(MCP),模拟生物神经元通过“阈值激活”处理信号,标志着神经网络理论的早期萌芽。

1958年,计算机科学家Frank Rosenblatt提出了感知器模型(Perceptron),感知器通过权重调整进行学习,是首个可训练的神经网络模型。虽然局限于处理二元线性分类问题,其已经具备现代神经网络模型中计算(前向传播)-判断(激活)-知错(计算误差/损失)-能改(权重修正)的基本思想。

尽管未显式计算梯度,感知器利用错误驱动学习的启发式权重更新规则已经暗示了梯度下降的思想。在感知器权重更新的过程中,误差信号为:
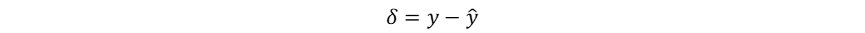
其与学习率α和输入本身共同完成权重调整:
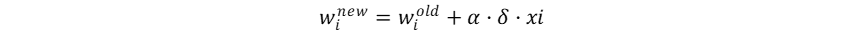
而如果在二分类问题中使用平方误差计算损失率:
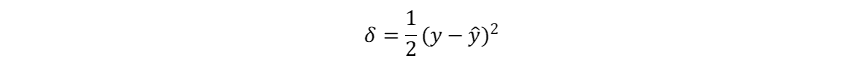
其梯度为:
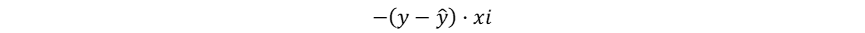
感知器调整权重的方式实际上符合梯度下降理论中减去梯度的要求,只是由于其未能显式定义损失函数且阶跃函数不可微,导致感知器始终局限于处理线性可分问题(Marvin Minsky和Seymour Papert在《感知机》一书中指出感知机无法解决非线性问题),直接导致了神经网络研究20年的漫长寒冬。
20世纪80年代,Rumelhart、Williams等人在输入层和输出层之间加入隐藏层(Hidden Layer),提出了多层感知器(MLP,Multilayer Perceptron),也称人工神经网络(ANN,Artificial Neural Network):

当多层感知器的隐藏层的数量超过三层时,也就成为了今天的深度神经网络(DNN,Deep Neural Network),其中每个神经元都具有加权计算+激活函数输出的功能,并且每一层神经元的输出都作为下一层神经元的输入:
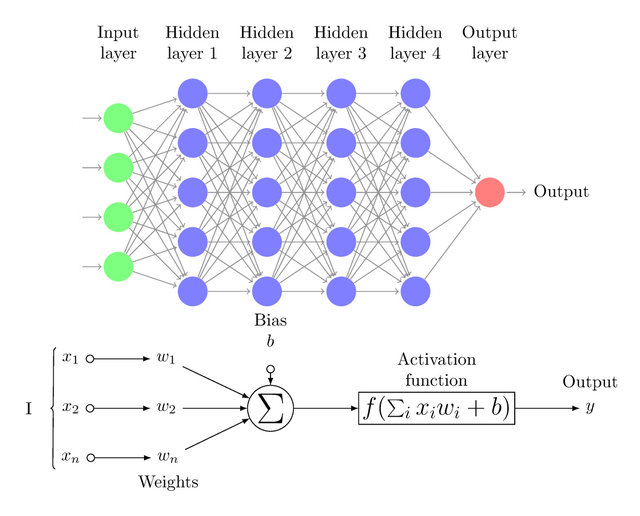
在多层感知器的发展过程中,非线性激活函数(如Sigmoid)被引入神经网络:

其图像是一个S形的平滑曲线:

非线性激活函数将线性组合z=Wx+b映射到非线性区间 (0,1),自此神经网络开始能够解决线性不可分问题。其引入非线性的同时,也引入了可导性,为反向传播的提出奠定了基础:
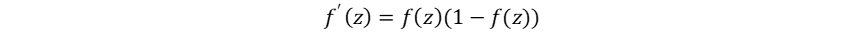
在1986年,Rumelhart、Hinton和Williams提出反向传播(Backpropagation),其数学本质是计算损失函数 L对所有权重系数W和偏置系数b的梯度 ∂L/∂W 和 ∂L/∂b,通过复合函数求导的链式法则将误差逐层传播到所有权重系数和偏置系数。反向传播作为一个更普适、在数学上更严谨的优化框架,能够有效训练多层神经网络,推动了多层感知器的发展。
以3层MLP 为例(输入层(0)→隐藏层(1)→输出层(2)),设置损失函数为均方误差:
| 符号 | 含义 |
|---|---|
| x | 输入向量 |
| W(1),b(1) | 输入层→隐藏层的权重和偏置 |
| z(1)=W(1)x+b(1) | 隐藏层的加权输入 |
| a(1)=σ(z(1)) | 隐藏层激活输出(σ为激活函数) |
| W(2),b(2) | 隐藏层→输出层的权重和偏置 |
| z(2)=W(2)a(1)+b(2) | 输出层的加权输入 |
| a(2)=ϕ(z(2)) | 神经网络最终输出(ϕ为输出层激活函数) |
| L | 损失函数(如均方误差、交叉熵) |
(1)损失函数-输出层:
损失函数:
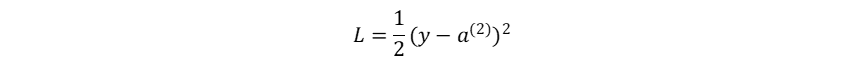
损失函数对神经网络最终输出的梯度:
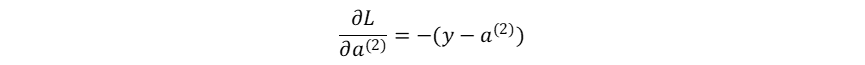
神经网络最终输出对输出层的加权输入的梯度:
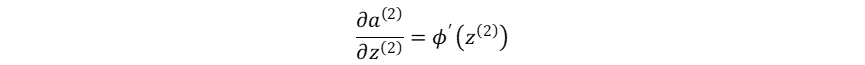
损失函数对输出层的加权输入的梯度:

(2)损失函数-输出层-隐藏层:
输出层加权输入对隐藏层→输出层权重系数的梯度:
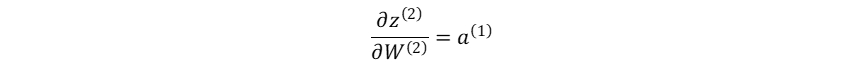
损失函数对隐藏层→输出层权重系数的梯度:

输出层加权输入对隐藏层→输出层偏置系数的梯度:
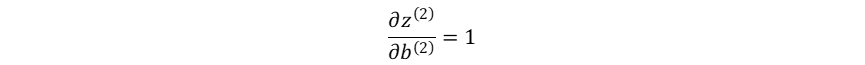
损失函数对隐藏层→输出层偏置系数的梯度:

(3)损失函数-输出层-隐藏层-输入层:
隐藏层的加权输入对输入层→隐藏层权重系数的梯度:
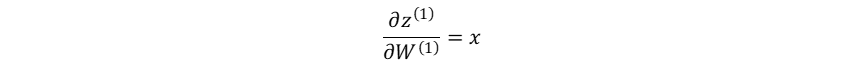
损失函数对输入层→隐藏层权重系数的梯度:
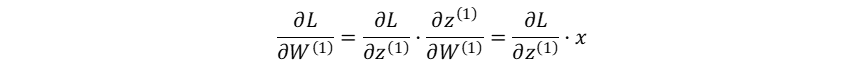
隐藏层的加权输入对输入层→隐藏层偏置系数的梯度:

损失函数对输入层→隐藏层偏置系数的梯度:

反向传播算法的提出,使得神经网络完成了从理论走向实践的关键转折,也为现代深度学习的多样化发展奠定了理论基础。其通过层级非线性变换逼近复杂函数的思想,至今仍是人工智能研究的核心范式。
神经网络相关理论的发展是问题导向的,每一次的突破都针对原先的不足而展开。McCulloch Pitts神经元模型解决了从无到有的问题;Rosenblatt感知器建立了神经网络知错-能改的思想框架;非线性激活函数的引入打破了线性操作的叠加性;反向传播算法的提出实现了误差的梯度更新。
反向传播算法的提出神经网络从理论迈向实践的转折点,MLP的局限性和潜力共同推动了后续的技术演进。为解决梯度爆炸、梯度消失和计算效率问题,研究者开始探索更贴合数据特性的结构创新:卷积神经网络(CNN)通过局部连接和权值共享,在图像处理中实现了参数精简与空间特征提取;循环神经网络(RNN)及其变体LSTM则针对序列建模引入时间维度记忆,但这些结构在深层训练时稳定性仍然不足;残差网络(ResNet)通过跨层跳跃连接重构梯度传播路径,使千层网络的训练成为可能,极大释放了深度学习的潜力。
除结构创新外,模型优化技术也得到了发展:动量法(Momentum)引入了历史梯度方向惯性,加速收敛并减少震荡;AdaGrad为不同参数分配不同学习率;Adam优化器则是动量加速与自适应学习率的结合;正则化技术如Dropout和批量归一化(BatchNorm)能够有效缓解过拟合,提升模型泛化能力。
再后来,生成对抗网络(GAN)和对比学习等理论的出现推动了无监督与自监督学习。Transformer架构以自注意力机制取代传统循环结构,解决了长依赖问题的同时,凭借并行计算优势成为自然语言与多模态任务的通用框架,如BERT、GPT、ViT等。
…

神经网络的本质和初衷在于对于人脑神经系统的模仿,其训练拟合、检验优化、测试修正进而开展判断识别、分类描述、推理预测的过程,在认识-实践的哲学意义上同样有着优美的表达,譬如说理论在实践中形成并得到检验,模型在训练中拟合并得到评估;譬如说理论具备普遍性的品格,要求了模型具有泛化能力;譬如说理论具备特殊性的品格,暗示了模型复杂多样的结构。在可预见的未来,在丰富计算资源和数据资源的支撑下,神经网络相关的研究必然进入一个更加勃勃生机、万物竞发的境界。
1.Rosenblatt感知器
Rosenblatt感知器是第一次实现完整算法描述和数学证明的神经元模型:

其结构主要包括:
(1)输入
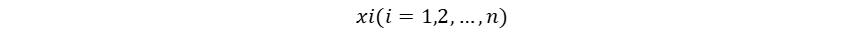
(2)权重

(3)独立偏置项b
(4)加权求和函数
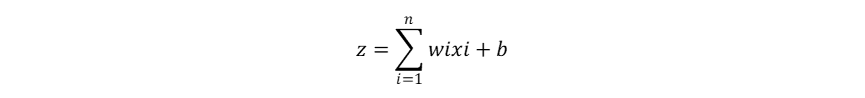
(5)激活函数
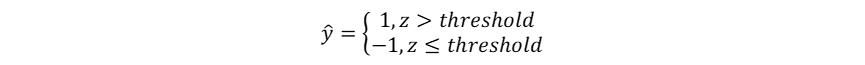
在以上结构中实现的是一次前向传播,若预测结果与真实标签不一致,则
(6)计算预测结果与真实值间的误差

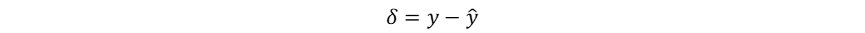
(7)引入学习率α控制参数调整步长,更新权重系数

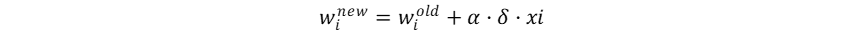
(8)更新独立偏置系数
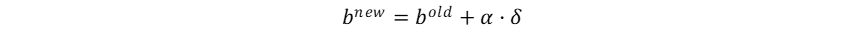
在达到预设的最大迭代次数或者误差小于某个阈值、权重更新量小于某个阈值之前,上述步骤不断重复迭代,由此不断调整权重和偏置,使得感知器的输出能够尽可能接近真实标签,从而实现对输入数据的分类。
Rosenblatt感知器概念的提出显然具备里程碑式的意义,其在非线性可分问题上的局限性,既是神经网络研究20年漫长寒冬的根源,也促使后来的研究者引入非线性激活函数,提出梯度下降等概念,使得神经网络从简单的线性分类器进化成为能够处理复杂非线性问题的强大模型。